
SAS2024 in Taiwan – final deadline approaching
If you have a chance to travel to Taiwan this autumn, you’ll be able to enjoy the SAS2024 conference! It has been two years since […]

If you have a chance to travel to Taiwan this autumn, you’ll be able to enjoy the SAS2024 conference! It has been two years since […]
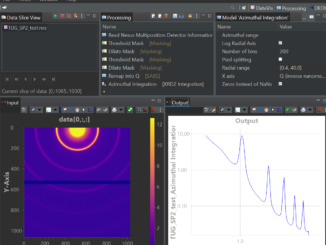
One persistent problem in the X-ray scattering community is the lack of data interoperability. This is exactly what kicked off the CanSAS collaboration 40 years […]

During the last four weeks, we’ve had a guest visiting the lab from the University of Washington. Abdul Moeez, a Ph.D. student in Prof. Lilo […]
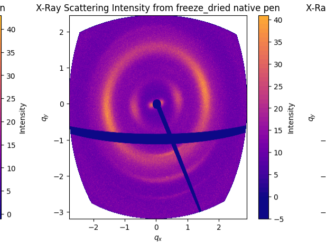
Besides the ongoing instrument migration efforts, we are also continuing work on “real” science. One of these involves the backbone of squid (called a squid […]

Regular readers will know we are in the process of migrating away from the last vestiges of the original SPEC-based control system on our (already […]

Two weeks ago, I was at a winter school on “Metrology and Nanomaterials for Clean Energy”, to present on the 1200 traceable MOF syntheses as […]

When it became time to build a new temperature controller, I wanted to build an ultimate design that could be used for (almost) everything. This […]
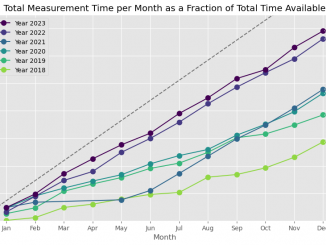
Are you curious how much you can gain by automating of your methods and instrumentation? The operational stats for the MOUSE including 2023 are now […]

We’re already 2% into 2024, but there might still be time to wish you a happy new year, and hint towards the plan for 2024. […]
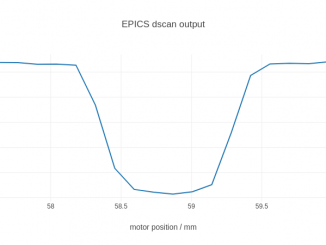
After about 1.5 months of struggles with the collapse of the veritable domino-stack of hardware that comprises the MOUSE, the system is now functional to […]
Copyright © 2024 | WordPress Theme by MH Themes