About SA(X)S

If you are not familiar with small-angle scattering, this may be a good place to start.

update: check out this review paper, which discusses most aspects of SAXS data collection, all possible data correction steps and has a few remarks on the subsequent data fitting steps. Besides this introductory text, there is also a good write-up here, which is a little more in-depth and expansive.

Welcome to small-angle scattering. Techniques such as light scattering (LS), small-angle x-ray scattering (SAXS) and small-angle neutron scattering (SANS) are all small angle scattering techniques. These techniques are used to analyse the shape and size of objects much smaller than can be seen by eye, by analysing the way that radiation (light, x-rays or neutrons) is scattered by the objects. The sizes we are talking about range from 1 micrometer to several angstrom (1 angstrom is 1x10^-10 meters, or 0.0000000001 meter). Unlike microscopic techniques, in small-angle scattering, the smaller the size, the easier it is to measure. There are other marked differences with microscopy, which will be discussed after explaining what the technique is.

All aforementioned scattering techniques operate on the principle of wave interference when contrasting features are encountered in the sample. No photon energy loss is assumed in most cases, so that all scattering effects can be considered purely elastic. And can be treated as a pure wave-interference effect.

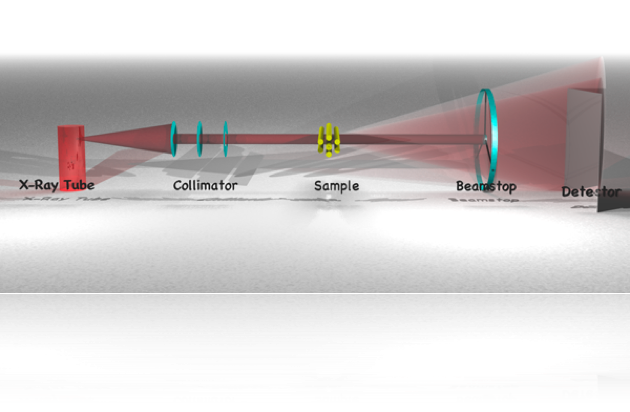
For the technique to work, a beam of parallel ‘light’ is shone upon a sample. Small contrasting features cause a fraction of the light to deviate from its path, thus scattering. This scattered light is then collected on an angle-discriminating detector.

As mentioned, scattering occurs when contrasting features are present. This has implications to the type of samples that can be measured. Among the samples that can be analysed with small-angle scattering are proteins in solution, polydisperse particles, pore structures and density differences in single-phase samples. What is important is that there is a contrast between the particle or pore, and the surrounding material in the sample. The type of contrast varies depending on the type of radiation used. In small-angle x-ray scattering this is an electron density contrast, for small-angle neutron scattering this is a neutron scattering cross-section, and for small-angle light scattering this is a transmittance contrast. This difference in contrast type means that if there is a contrast problem while measuring a sample with one technique (i.e. too little or too much contrast), by switching to a different radiation type you may be able to solve your problems.

Like its sister technique, diffraction, small-angle scattering charcterises lengths in a sample. Simply said, small objects scatter a little to larger angles, and large objects scatter a lot to small angles. Since the scattering behaviour is highly dependent on the lengths in the sample, this length information can (in most cases) be retrieved.
A variety of analysis methods can be used to interpret the scattering behaviour.

These analysis methods revolve around a mathematical construct known as the Fourier transform. Effectively, the scattering can be calculated as the Fourier transform of the real-space structure. In other words, a measurement is a physical Fourier transform of your sample. Unfortunately, most detectors can only measure the intensity of the Fourier transform, and not its complementary phase information, and thus vital information is lost, complicating data interpretation.

A marked differences from diffraction techniques is that the small-angle scattering pattern does not contain much information. Indeed, without information on the sample morphology obtained from other techniques such as microscopy, the small-angle scattering information is open to a multitude of interpretations (technically, this is true of diffraction as well, but methods have been developed to get around this problem for some diffraction data). So why would we choose to use this technique as opposed to, say, microscopic methods?

Comparison with microscopy techniques
Microscopy methods are the first techniques that come to mind when faced with a problem involving the analysis of small particles, and for good reasons. Microscopy allows for visualisation of objects of virtually any size below a centimeter or so. Optical and confocal microscopes can image objects to sub-micron resolution. Scanning electron microscopes image down to several hundred nanometers, and transmission electron microscopes go even further down, sometimes to near-atomic resolution. Scanning-probe microscopes can probe along the entire size-range. (For sizes comparable to those probed by small-angle scattering techniques, optical microscopy is often not an option and will not be considered beyond this point.)

But if you talk to microscopists, you will find that one of the bigger challenges in the successful application of microscopy lies in the sample preparation. The further down you want to go in size, the more complex the preparation can become, and many (soft) samples can therefore not be measured properly. The sample preparation method may also induce a structure in the sample, for example due to stresses imposed during cutting, grinding or polishing. This can make it difficult to distinguish the sample structure from the induced artefacts.

But even if the sample preparation is done perfectly, you can only observe a small fraction of the complete sample at a time. In order to get a good statistical average, you need to prepare many samples and measure each sample at multiple locations. This is far from impossible, but it makes you start to think if there would be another solution to your problem.

Finally, if you are interested in observing your sample in-vivo or in-situ, e.g. under reaction conditions or high pressure, microscopic techniques ofen fail to offer solutions.

With small-angle scattering, these problems are substituted for others (which we will come to in a minute). Firstly, small-angle scattering requires only very little, if any, sample preparation. Liquid samples can be measured in capillaries, for example, and fibre samples can be measured simply by suspending the fibre in the beam. Many in-situ reactors can also be used so that reactions can be probed as they proceed.

An additional benefit is that the information present in the scattering pattern pertains to all objects in the irradiated volume. This means that if you want to get an average particles parameter over billions of particles in a suspension, all you need to do is make sure the irradiated sample volume is large enough to contain a billion particles. In small-angle x-ray scattering, volumes of about one to several cubic millimeters are commonly probed. For neutron scattering techniques, this irradiated volume is usually a cubic centimeter or more!

So there are certainly advantages of using small-angle scattering methods over microscopes methods, yet microscopes dominate laboratories. Why is that? That is related to the challenges of analysis of small-angle scattering patterns, and the challenges of collecting a good scattering pattern.

Challenges with small angle x-ray scattering
Please excuse my focus in this case on x-ray scattering, it is simply the form of scattering I am most familiar with. Some challenges, but not all, of x-ray scattering can be translated to the other scattering techniques.

There are many fine details about the challenges of SAXS. Besides the challenges of collecting a near-perfect scattering pattern (which in many cases can be overcome through hard work and understanding), the main issue lies with the data analysis.

If you have managed to collect the perfect background-subtracted scattering pattern in the right angular region on an absolute scale with uncertainties for each data point, the road ahead may still be unclear. The problem lies mainly in the ambiguity of the data, which has become ambiguous since we have lost information in the scattering process (as we have detected only the scattering intensity and have lost the phase information of the Fourier transform). The most clear example of this loss is that particle shape and polydispersity can no longer both be retrieved.

This is another important concept in scattering; you can only determine the polydispersity if you know the particle shape, and you can only determine the particle shape if you have information on the polydispersity (for example if you have a monodisperse sample of proteins in solution, or if you have information on the distribution shape). This means experimentally that, in order to get convincing results of your SAXS data analysis, you need complementary microscopy information. Even with all the information, data fitting is difficult at best.

In short then, the technique is still (a hundred years after conception) in dire need of development, mostly in terms of data analysis. This weblog aims to collect some of the information on the web for other users and developers, and adding a bit more of my own research, in the hope that we can get closer to making small-angle scattering easy.

under construction