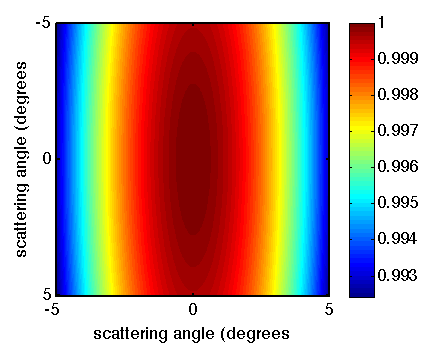
Does it matter part 2: polarization factor and spherical corrections
In this series of posts, we take a quick look at some uncommon corrections you can do to your scattering patterns and we evaluate whether […]
Measurement Technique
Baby, and the perfect measurement made easier
I apologise for my low activity in the last few weeks. Those of you who are following my Twats (Twitter messages) will probably be able […]
Does it matter? part 1: sample direction-dependent absorption
This series is part of a set to determine which corrections matter when. We all heard -or read- about corrections Small-angle Scatterers do not need […]
Work in Progress: How to do a SAXS measurement well
Hi all. For a work-related project, I have been developing some software and writing some documentation. This documentation is still a work in progress (as […]