
Nothing new here
So it seems science has beaten us to the punch once again. Remember last week’s optimistic story on how you can make better use of […]

So it seems science has beaten us to the punch once again. Remember last week’s optimistic story on how you can make better use of […]
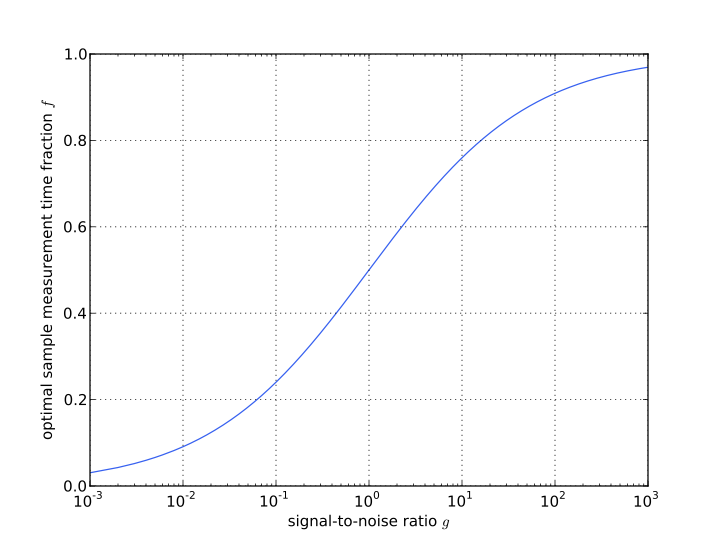
Often, especially when measuring on big facilities, you are given a limited amount of time. So when it comes to measuring the sample and the […]
Copyright © 2024 | WordPress Theme by MH Themes