Nothing new here
So it seems science has beaten us to the punch once again. Remember last week’s optimistic story on how you can make better use of […]
scattering
Making better use of your time: optimizing measurement time
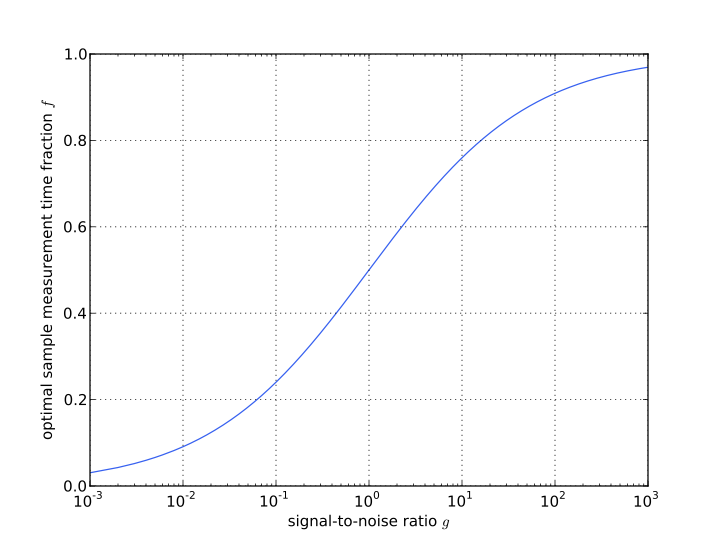
Often, especially when measuring on big facilities, you are given a limited amount of time. So when it comes to measuring the sample and the […]
A compact pneumatic fibre tensile stage – publication
It is with pleasure that I can announce the publication of another fibre-related work, right here (The electronic reprint will be made available after December on […]
Live FT video
A demonstration of the live Fourier Transform showing scattering patterns can be seen here:
More Youtube videos
So, I could not do what I promised last time, the Monte-Carlo fitting works on perfect simulated scattering patterns but is as of yet unable […]
“Perfect” 1D pattern generation software.
I have written some small, simple bits of Matlab software that can generate scattering patterns in the range you request for polydisperse, dilute spheres or […]