Nothing new here
So it seems science has beaten us to the punch once again. Remember last week’s optimistic story on how you can make better use of […]
statistics
Making better use of your time: optimizing measurement time
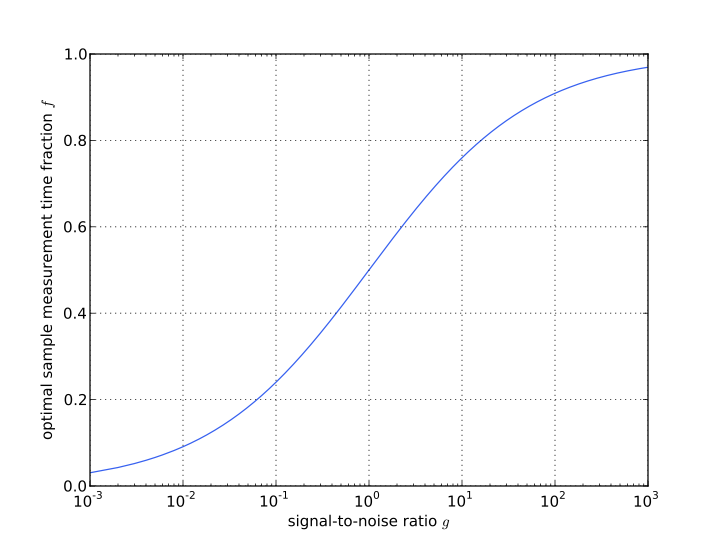
Often, especially when measuring on big facilities, you are given a limited amount of time. So when it comes to measuring the sample and the […]
More statistics and change of job
Hello dear readers, As a followup on my previous story, a colleague of mine sent me this paper that helps explain the standard deviation, standard […]
Everybody hates statistics…
Everybody hates statistics [1]… … but it can be of major importance in our small angle world. While very few papers on small-angle scattering […]