Avoid these issues when designing synchrotron experiments…
This year, I’ve become part of a peer review panel. These are panels that wade through a long list of proposals for beamlines, and rank […]
teaching
Presenting for Scientists – video
If you give bad presentations, you can kill people. If you want to find out why, and get some tips on presentation techniques (the ones […]
Does it matter part 2: polarization factor and spherical corrections
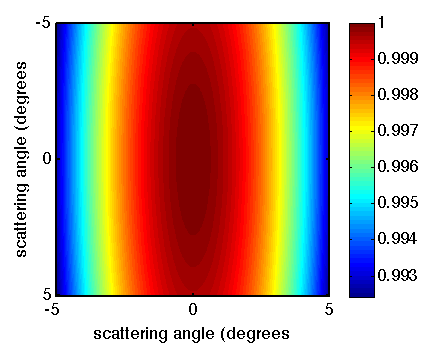
In this series of posts, we take a quick look at some uncommon corrections you can do to your scattering patterns and we evaluate whether […]
Does it matter? part 1: sample direction-dependent absorption
This series is part of a set to determine which corrections matter when. We all heard -or read- about corrections Small-angle Scatterers do not need […]
Live FT video
A demonstration of the live Fourier Transform showing scattering patterns can be seen here:
Live Fourier transform
During some recent presentations, I have used a small matlab program giving me a live Fourier transform of the laptop camera input. It can be […]
Errors and improvements in the perfectpattern code
Hi all, Just a quick heads-up, there are some minor errors in the perfectpattern code with respect to the convergence criteria. Also I have made […]
Notes on Guinier
…well, his famous SAXS analysis method. This documentGuinier_short, copyright Brian Pauw gives a short description and review of the applicability of the Guinier method to […]
More Youtube videos
So, I could not do what I promised last time, the Monte-Carlo fitting works on perfect simulated scattering patterns but is as of yet unable […]
Teaching and how it applies to us.
We teach. Every one of us. If we have a classroom of students, it is obvious, but also when we talk to colleagues, we sometimes […]